外观
约束满足问题
一、定义与核心思想
约束满足问题是人工智能和运筹学中的一类组合优化问题，旨在为一组变量寻找满足所有约束条件的赋值。其核心特征包括：
- 变量集合：需赋值的对象（如地图着色中的地区、排班中的员工）。
- 值域集合：每个变量可能的取值范围（如颜色集合{红、绿、蓝}）。
- 约束集合：变量间的限制条件（如相邻地区颜色不同）。
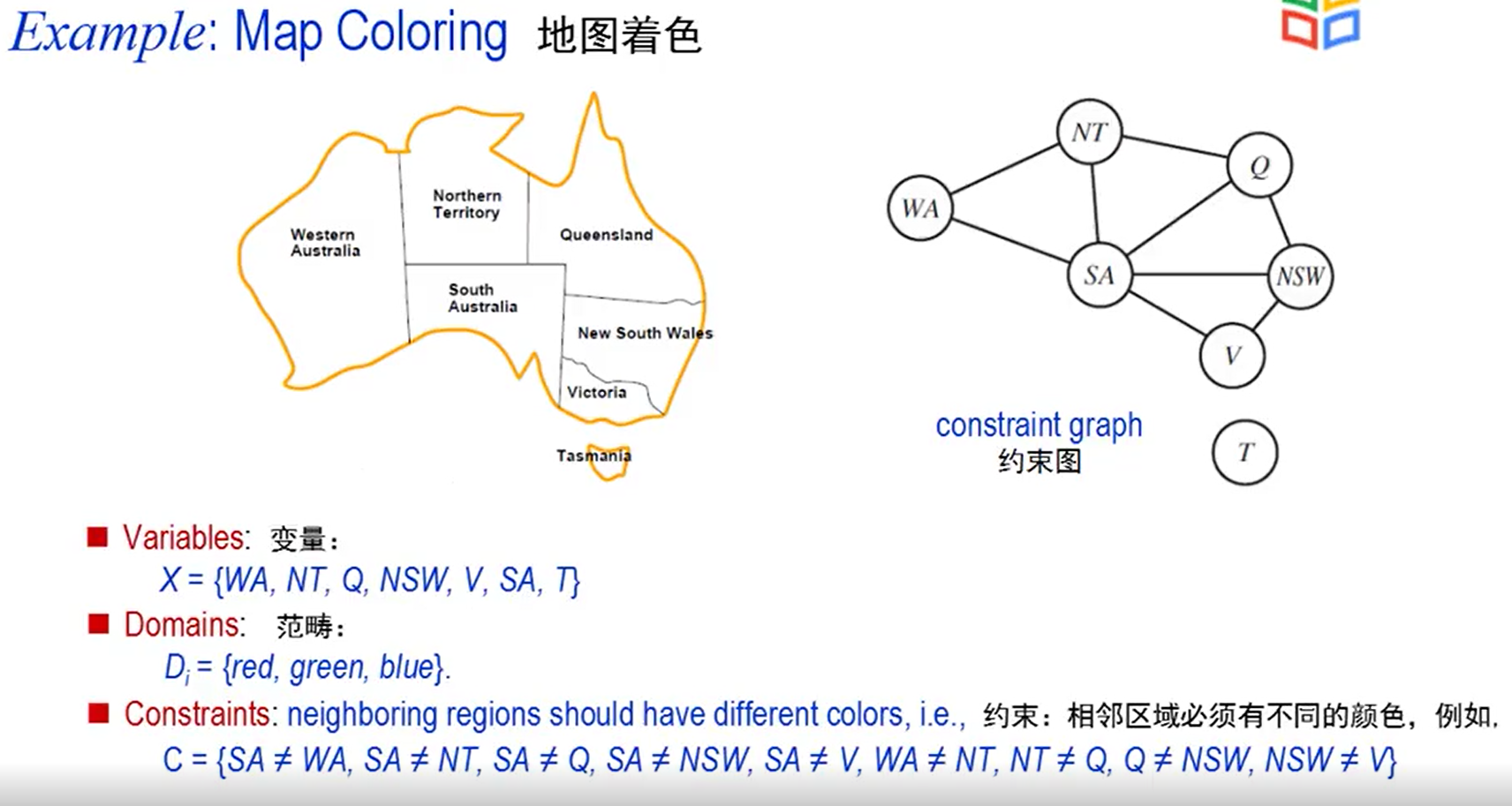
经典示例：
- 地图着色问题：为澳大利亚各州分配颜色，确保相邻州颜色不同（变量为州名，约束为相邻颜色差异）；
- 数独游戏：每个数字在行、列、宫格内唯一（Alldiff全局约束）。
二、CSP的核心组成与建模
1. 变量与值域
- 离散型变量：如地图着色中的颜色选择，值域为有限集合；
- 连续型变量：如天文观测时间安排，值域为实数区间；
- 混合型变量：部分变量离散、部分连续（如物流调度中的车辆类型与出发时间）。
2. 约束类型
| 约束类型 | 描述 | 示例 |
|---|---|---|
| 一元约束 | 限制单个变量的值域（如“南澳大利亚不可用绿色”） | 员工排班中的技能限制 |
| 二元约束 | 涉及两个变量的关系（如相邻地区颜色不同） | 地图着色、密码算术游戏 |
| 全局约束 | 涉及多个变量的复杂关系（如Alldiff约束要求所有变量取值不同） | 数独、密码算术问题 |
| 偏好约束 | 非强制约束，但优化目标（如教师偏好下午上课） | 排班中的时间偏好 |
三、CSP求解方法
1. 回溯搜索（Backtracking Search）
- 基本流程：深度优先遍历变量赋值，遇到冲突时回溯；
- 优化策略：
- 最小剩余值（MRV）：优先选择可选值最少的变量，减少搜索分支；
- 度启发式：优先约束最多的变量，降低后续冲突概率；
- 最少约束值：选择对后续变量限制最小的值。
2. 约束传播（Constraint Propagation）
- 前向检验（Forward Checking）：赋值时删除相邻变量的冲突值域，提前发现矛盾；
- 弧相容（Arc Consistency）：确保每对变量的每个值都存在相容的对应值；
- 路径相容：扩展至多变量约束，检测高阶矛盾（如三州颜色连环冲突）。
3. 局部搜索（Local Search）
- 基本思想：从完全赋值出发，逐步调整减少冲突；
- 优化技术：
- 禁忌搜索：记录近期状态避免循环；
- 模拟退火：允许暂时接受次优解以跳出局部最优；
- 冲突加权：优先解决难以满足的约束。
4. 问题结构优化
- 独立子问题分解：将大规模CSP拆分为互不影响的子问题（如多区域分块着色）；
- 树形结构处理：对无环约束图设计线性时间复杂度算法。
四、应用领域与实例
1. 传统组合优化
- 排班调度：医院护士排班需满足技能、工时、偏好约束；
- 物流规划：车辆路径优化（时间窗、载重约束）；
- 产品配置：计算机定制需兼容硬件参数。
2. 游戏与密码学
- 数独与密码算术：通过Alldiff约束求解唯一解；
- 瑞巴攻击防御：利用CSP模型检测网络通信中的异常重放行为（如时间戳连续性验证）。
3. 复杂系统设计
- 芯片布线：电路信号路径需满足电气与空间约束；
- 天文观测调度：哈勃望远镜任务需协调时间、能源与优先级。
五、挑战与优化方向
1. 计算复杂度
- 指数爆炸：变量数与分支因子导致搜索空间呈指数增长（如n皇后问题复杂度O(nⁿ)）；
- 优化策略：剪枝算法（Alpha-Beta）、并行计算（GPU加速）。
2. 动态与不确定性
- 实时调整：物流调度中突发需求变更需在线重规划；
- 概率约束：引入模糊逻辑处理不完全信息（如天气预报影响排班）。
3. 混合问题扩展
- 连续-离散混合：如供应链优化中的库存量（连续）与运输方式（离散）协同；
- 多目标优化：平衡成本、时间与碳排放等冲突目标。
六、总结
约束满足问题通过变量、值域与约束的形式化建模，成为解决复杂现实问题的通用框架。其核心价值在于将多样化的实际需求（如地图着色、网络安全）转化为可计算的数学问题，并通过回溯、传播与启发式策略高效求解。未来，结合量子计算与深度学习的混合CSP算法，有望在超大规模优化与动态场景中实现突破。
版权所有
版权归属：